21.9 Alternativas

21.9.1 Transformación (modelos linealizables)

Cuando no se satisfacen los supuestos básicos se puede intentar transformar los datos para corregir la falta de linealidad, la heterocedasticidad y/o la falta de normalidad (normalmente estas últimas “suelen ocurrir en la misma escala”). Por ejemplo, la función boxcox del paquete MASS permite seleccionar la transformación de Box-Cox más adecuada: \[Y^{(\lambda)} = \begin{cases} \dfrac{Y^\lambda - 1}{\lambda} & \text{si } \lambda \neq 0 \\ \ln{(Y)} & \text{si } \lambda = 0 \end{cases}\]

# library(MASS)
boxcox(modelo)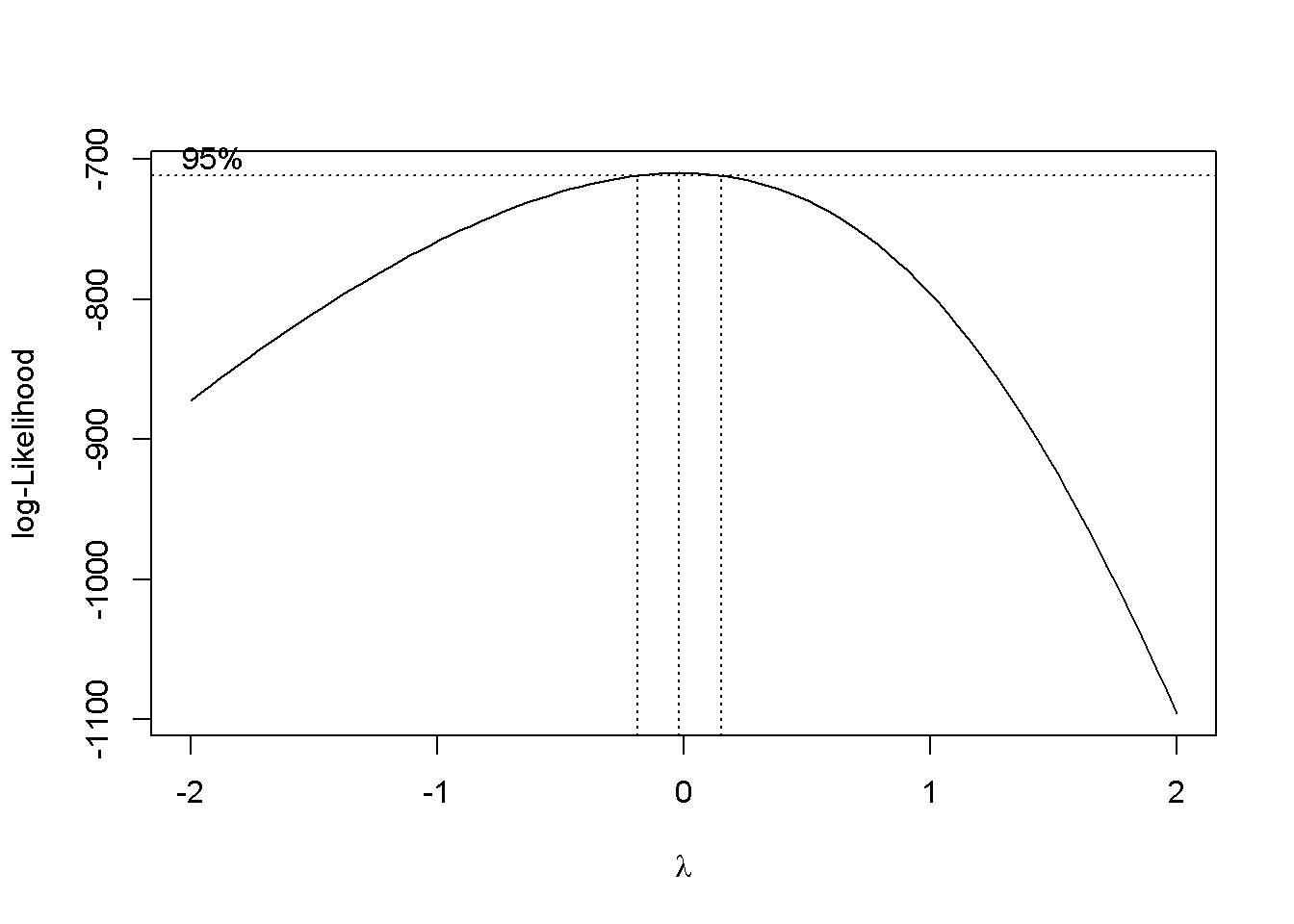

En este caso una transformación logarítmica parece adecuada.

En ocasiones para obtener una relación lineal (o heterocedasticidad) también es necesario transformar las covariables además de la respuesta. Algunas de las relaciones fácilmente linealizables se muestran a continuación:

modelo	ecuación	covariable	respuesta
logarítmico	\(y = a + b\text{ }log(x)\)	\(log(x)\)	_
inverso	\(y = a + b/x\)	\(1/x\)	_
potencial	\(y = ax^b\)	\(log(x)\)	\(log(y)\)
exponencial	\(y = ae^{bx}\)	_	\(log(y)\)
curva-S	\(y = ae^{b/x}\)	\(1/x\)	\(log(y)\)

21.9.1.1 Ejemplo:

plot(salario ~ salini, data = empleados, col = 'darkgray')

# Ajuste lineal
abline(lm(salario ~ salini, data = empleados)) 

# Modelo exponencial
modelo1 <- lm(log(salario) ~ salini, data = empleados)
parest <- coef(modelo1)
curve(exp(parest[1] + parest[2]*x), lty = 2, add = TRUE)

# Modelo logarítmico
modelo2 <- lm(log(salario) ~ log(salini), data = empleados)
parest <- coef(modelo2)
curve(exp(parest[1]) * x^parest[2], lty = 3, add = TRUE)

legend("bottomright", c("Lineal","Exponencial","Logarítmico"), lty = 1:3)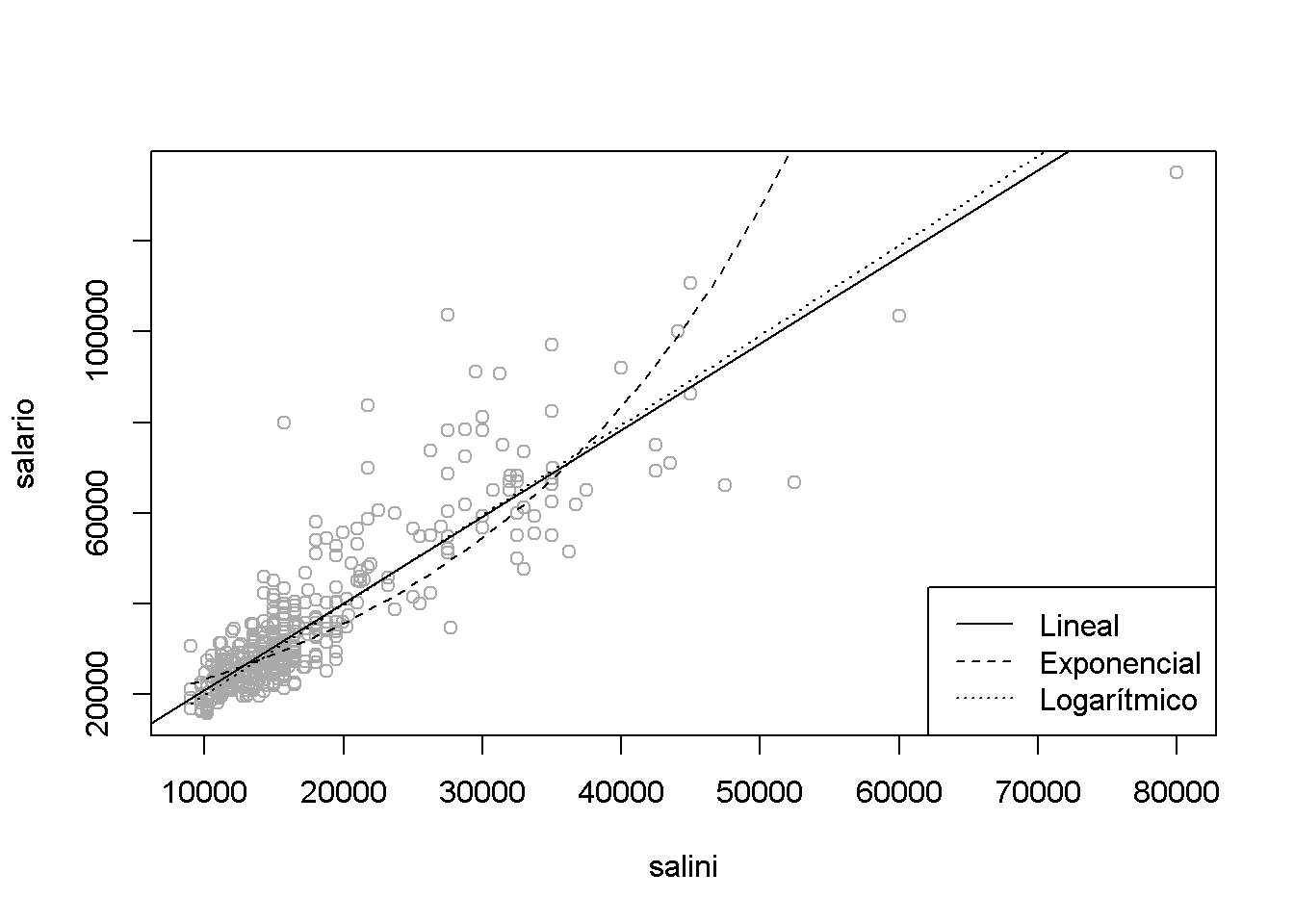

Con estos datos de ejemplo, el principal problema es la falta de homogeneidad de varianzas (y de normalidad) y se corrige sustancialmente con el segundo modelo:

plot(log(salario) ~ log(salini), data = empleados)
abline(modelo2)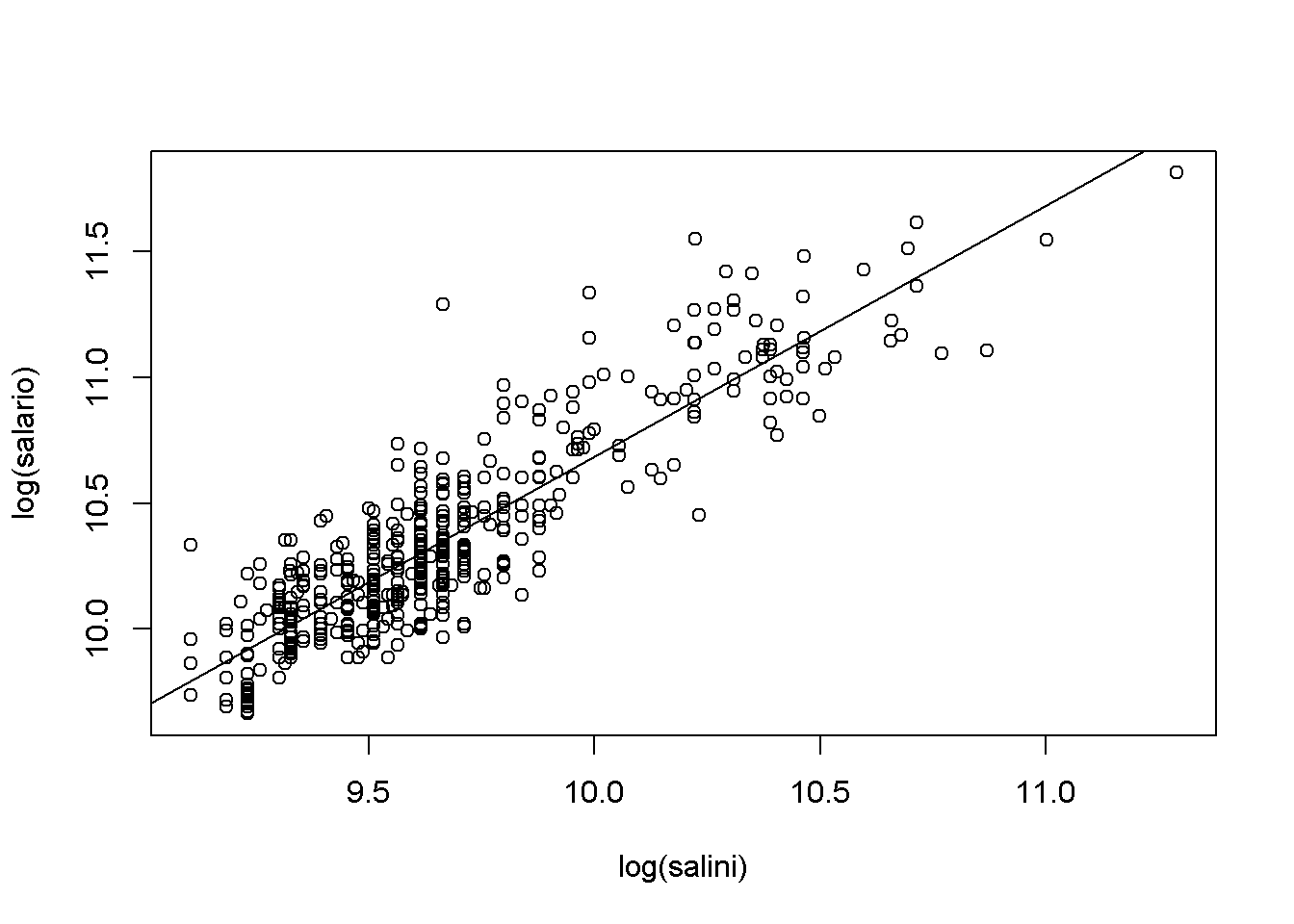

21.9.2 Ajuste polinómico

En este apartado utilizaremos como ejemplo el conjunto de datos Prestige de la librería car. Al tratar de explicar prestige (puntuación de ocupaciones obtenidas a partir de una encuesta ) a partir de income (media de ingresos en la ocupación), un ajuste cuadrático puede parecer razonable:

# library(car)
plot(prestige ~ income, data = Prestige, col = 'darkgray')
# Ajuste lineal
abline(lm(prestige ~ income, data = Prestige)) 
# Ajuste cuadrático
modelo <- lm(prestige ~ income + I(income^2), data = Prestige)
parest <- coef(modelo)
curve(parest[1] + parest[2]*x + parest[3]*x^2, lty = 2, add = TRUE)

legend("bottomright", c("Lineal","Cuadrático"), lty = 1:2)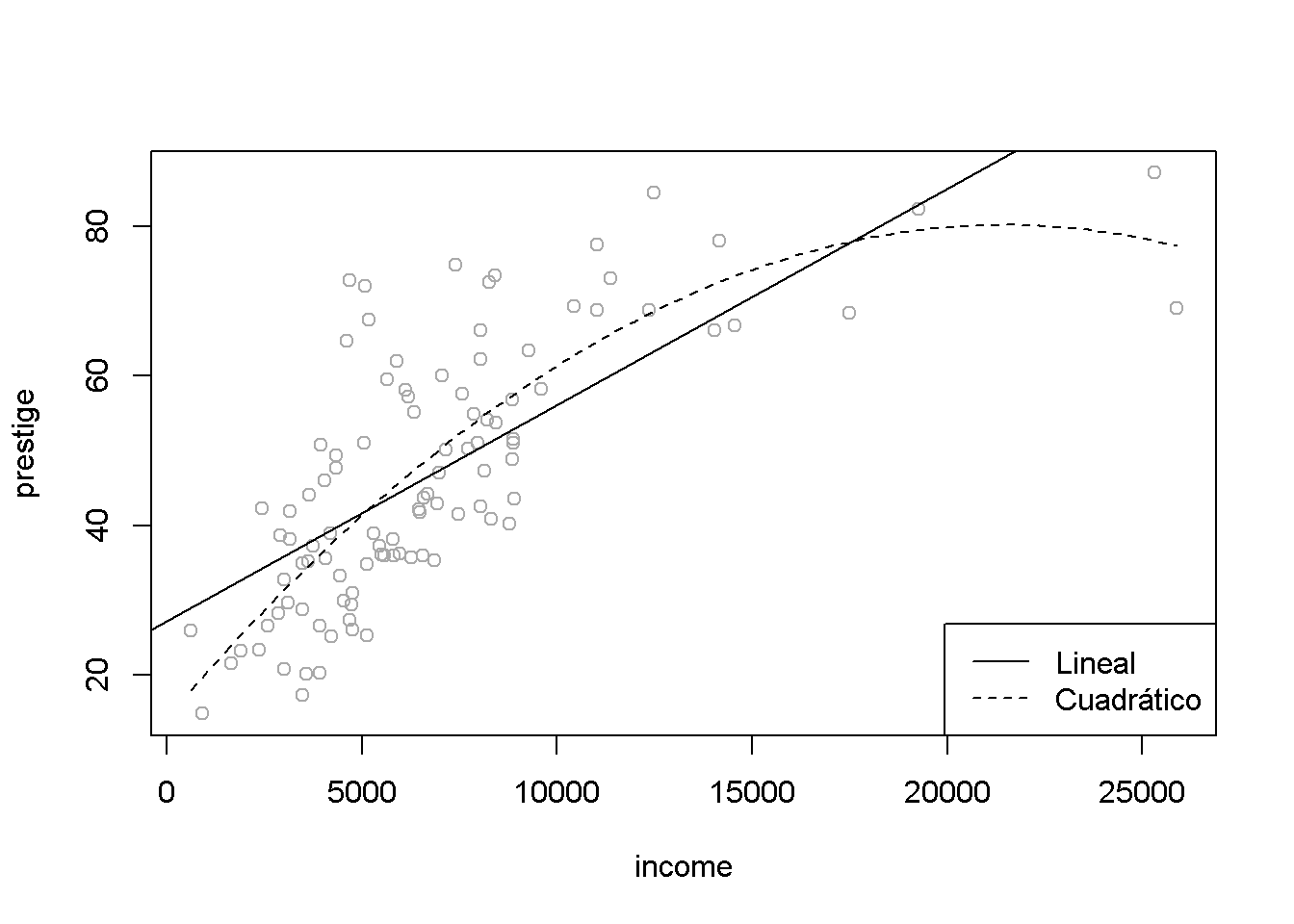

Alternativamente se podría emplear la función poly:

plot(prestige ~ income, data = Prestige, col = 'darkgray')
# Ajuste cúbico
modelo <- lm(prestige ~ poly(income, 3), data = Prestige)
valores <- seq(0, 26000, len = 100)
pred <- predict(modelo, newdata = data.frame(income = valores))
lines(valores, pred, lty = 3)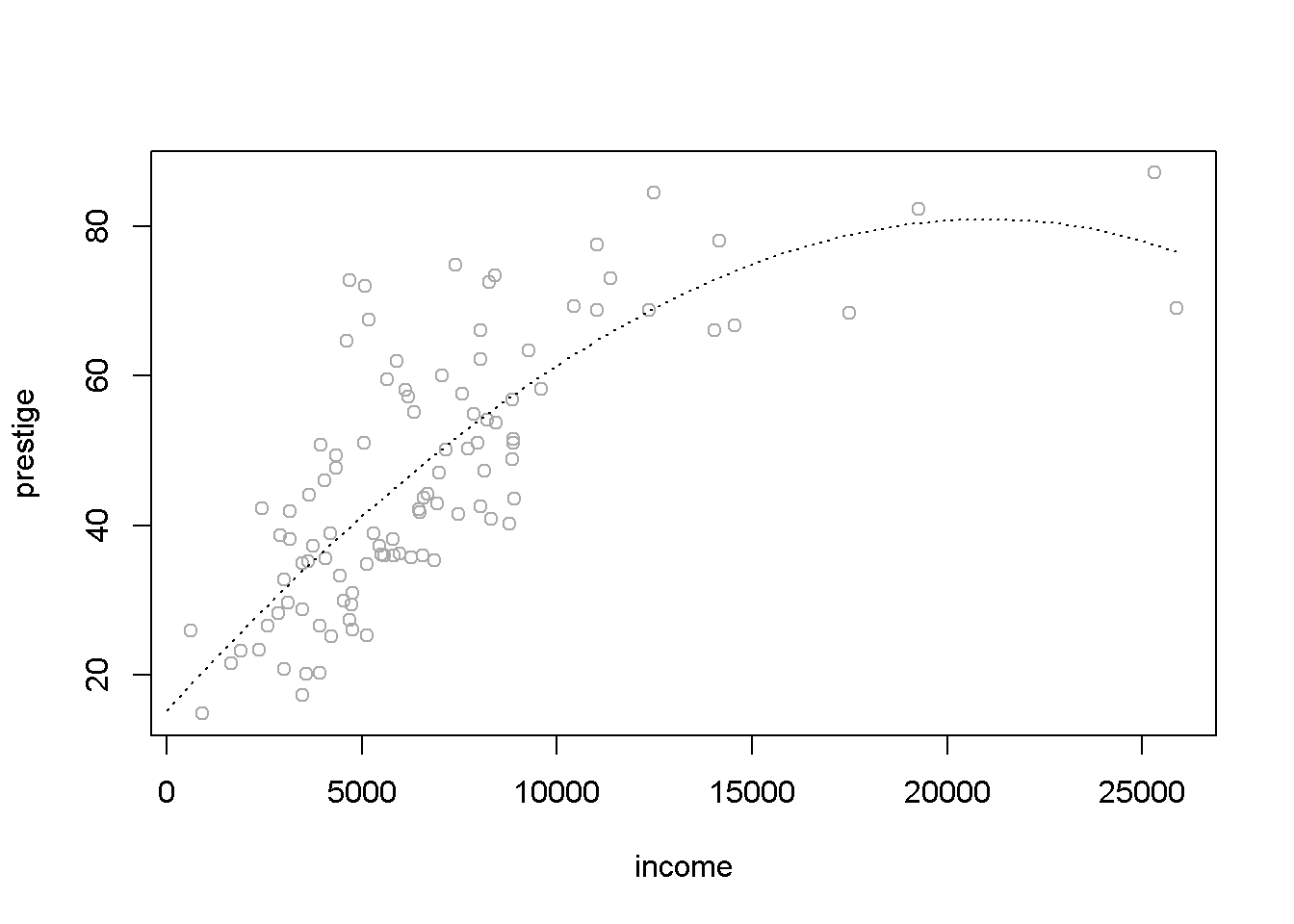 

21.9.3 Ajuste polinómico local (robusto)

Si no se logra un buen ajuste empleando los modelos anteriores se puede pensar en utilizar métodos no paramétricos (p.e. regresión aditiva no paramétrica). Por ejemplo, enR es habitual emplear la función loess (sobre todo en gráficos):

plot(prestige ~ income, Prestige, col = 'darkgray')
fit <- loess(prestige ~ income, Prestige, span = 0.75)
valores <- seq(0, 25000, 100)
pred <- predict(fit, newdata = data.frame(income = valores))
lines(valores, pred)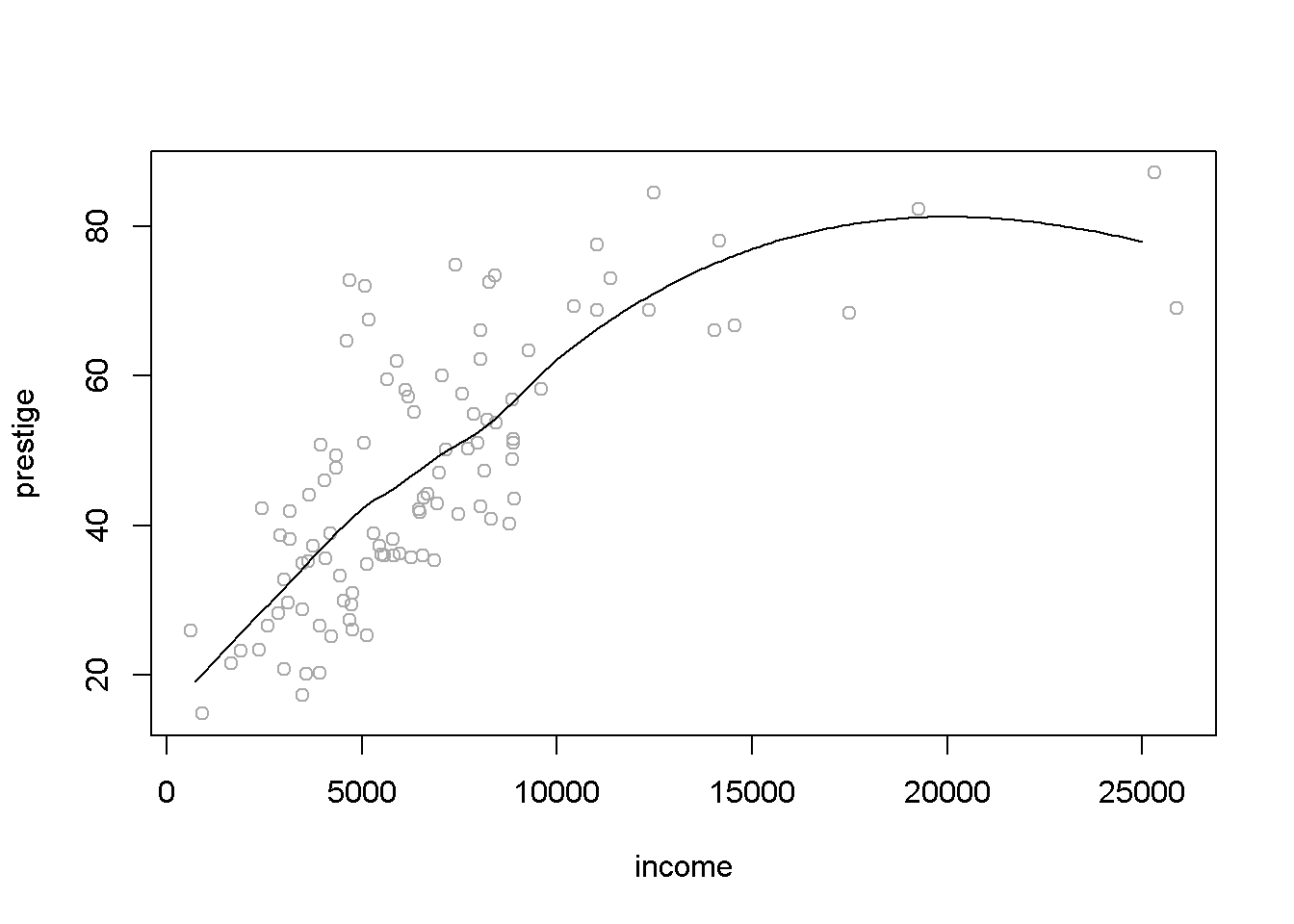

Este tipo de modelos los trataremos con detalle más adelante…